O que é o teste de hipóteses

No mundo atual, onde decisões — seja na ciência, nos negócios ou na educação — dependem cada vez mais de dados, saber diferenciar informações confiáveis de coincidências é essencial. Os testes de hipóteses oferecem exatamente essa ferramenta: permitem transformar observações e intuições em conclusões objetivas, baseadas em evidências. Com eles, é possível identificar padrões reais, reduzir erros e tomar decisões mais seguras e fundamentadas.

O papel dos testes de hipótese na tomada de decisões baseadas em dados

Ao explorar uma ideia — como a hipótese de que alunos que estudam pela manhã têm desempenho superior aos que estudam à noite — não é necessário examinar todos os indivíduos de um grupo. Os testes de hipótese permitem avaliar se o padrão identificado nos dados reflete um efeito real ou se poderia ter surgido por acaso.

Esses testes convertem suposições em métricas concretas, oferecendo uma base objetiva para determinar a existência de um efeito. Dessa forma, pesquisadores e profissionais conseguem tomar decisões fundamentadas em evidências, em vez de se apoiar apenas em impressões ou intuições.

Por que os testes de hipóteses são importantes

Os testes de hipóteses são ferramentas fundamentais para transformar observações em conclusões confiáveis. Eles fornecem um caminho estruturado para determinar se um resultado reflete um efeito verdadeiro ou se poderia ser explicado pelo acaso, evitando interpretações precipitadas ou enganosas.

Apoio à tomada de decisão

Em contextos científicos, empresariais ou de análise de dados, decisões muitas vezes envolvem riscos. Seja ao avaliar um novo medicamento, implementar mudanças em processos, lançar campanhas de marketing ou atualizar produtos, é necessário ter evidências robustas antes de agir. O teste de hipótese ajuda a quantificar esse risco, mostrando se o efeito observado é consistente o suficiente para justificar a mudança.

Redução de erros

Dados podem apresentar padrões que parecem significativos, especialmente em amostras pequenas ou heterogêneas. Ao aplicar testes de hipótese, diminui-se a probabilidade de aceitar conclusões baseadas apenas em flutuações aleatórias, proporcionando maior segurança na interpretação de diferenças, relações ou tendências.

Rigor científico

A ciência exige que os resultados sejam verificáveis e reproduzíveis. Os testes de hipótese estabelecem critérios objetivos para aceitar ou rejeitar uma hipótese, facilitando a replicação de estudos e fortalecendo a credibilidade das conclusões.

Versatilidade de aplicação

A ampla aplicabilidade dos testes de hipótese explica sua presença em diferentes áreas:

• Medicina: verificar se um tratamento produz efeito mensurável.
• Economia e políticas públicas: avaliar o impacto de medidas governamentais.
• Tecnologia e ciência de dados: testar modelos, validar algoritmos e conduzir experimentos A/B.
• Marketing: analisar se mudanças em campanhas ou produtos aumentam conversões.
• Educação: medir a eficácia de novas metodologias de ensino.

Distinguir padrões reais de coincidências

Ao examinar dados, é comum encontrar padrões que parecem significativos, mas que podem surgir apenas por acaso. Os testes de hipótese funcionam como uma lente, permitindo separar efeitos reais de ilusões estatísticas e entender não apenas se uma diferença existe, mas também sua relevância prática.

Principais tipos de testes de hipóteses

Os testes de hipóteses podem ser organizados de diferentes maneiras, dependendo do tipo de dado analisado e do objetivo da pesquisa. Uma classificação comum considera dois aspectos: se existem pressupostos sobre a distribuição dos dados e a direção da hipótese a ser testada.

Testes paramétricos

Os testes paramétricos são indicados quando os dados seguem uma distribuição conhecida, geralmente a normal. Além disso, exigem variâncias homogêneas entre os grupos e observações independentes. Entre os mais utilizados estão:

• Teste t — compara médias de um ou dois grupos.
• Teste z — aplicado quando o desvio-padrão populacional é conhecido.
• ANOVA — compara médias de três ou mais grupos.

Quando os pressupostos são atendidos, esses testes apresentam maior poder estatístico, aumentando a capacidade de detectar diferenças reais entre os grupos.

Testes não paramétricos

Os testes não paramétricos são indicados quando não é possível assumir uma distribuição específica para os dados, em casos de amostras com outliers ou quando se trabalha com variáveis ordinais, como escalas de satisfação, níveis de dor ou rankings subjetivos. Entre os exemplos mais comuns estão:

• Mann–Whitney U — compara dois grupos independentes.
• Wilcoxon — avalia medidas pareadas ou dependentes.

Embora geralmente apresentem menor poder estatístico que os testes paramétricos, esses métodos oferecem maior robustez quando os dados não atendem aos pressupostos clássicos, garantindo resultados mais confiáveis em situações complexas.

Testes unicaudais e bicaudais

Outra forma de classificação considera a direção da diferença avaliada:

• Unicaudais: verificam se um valor é maior ou menor que outro em apenas uma direção. Exemplo: “O novo medicamento reduz a pressão arterial?” — interessa apenas a redução, não o aumento. 
• Bicaudais: analisam diferenças em ambas as direções, tanto aumentos quanto reduções. Exemplo: “Há diferença de altura média entre homens e mulheres?” — qualquer diferença relevante é considerada.

Fórmulas teste de hipotese

Teste z: usado quando a população é normal e o desvio padrão populacional é conhecido.

​

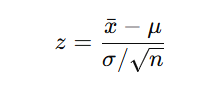
• x̄ — média da amostra
• μ — média populacional
• σ — desvio-padrão populacional
• n — tamanho da amostra

Teste t: indicado quando o desvio-padrão populacional é desconhecido ou a amostra é pequena.

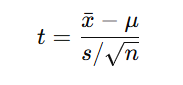
• s — desvio-padrão da amostra

Teste Qui-quadrado: aplicado a dados categóricos para comparar frequências observadas e esperadas.

​

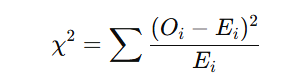
• Oi — frequência observada
• Ei — frequência esperada

ANOVA (estatística F): compara médias de três ou mais grupos, analisando a razão entre a variabilidade entre os grupos e dentro dos grupos.

Quanto maior essa razão, maior a indicação de diferença real entre as médias dos grupos.

Etapas de um teste de hipótese

A execução de um teste de hipótese segue uma sequência lógica que garante rigor e consistência na análise estatística. As etapas abaixo resumem o processo de forma clara e aplicada.

1. Definir H₀ e H₁

A primeira etapa é formular as hipóteses que serão avaliadas.

• H₀: afirma que não existe diferença ou efeito.
• H₁: propõe que a diferença ou efeito existe.

Exemplo:

• H₀: o medicamento não altera a pressão arterial.
• H₁: o medicamento altera a pressão arterial.

Definir essas duas afirmações com precisão evita interpretações equivocadas ao final do teste.

2. Escolher o nível de significância (α)

O nível de significância representa a probabilidade de rejeitar H₀ por engano — ou seja, cometer um erro do Tipo I. Valores frequentemente utilizados são 0,05 (5%) ou 0,01 (1%), dependendo do grau de rigor exigido.

3. Selecionar o teste estatístico adequado

A escolha do teste depende de fatores como:

• tipo de variável (numérica, categórica, ordinal);
• número de grupos a serem comparados;
• presença ou não de pressupostos de normalidade;
• tamanho da amostra.

Selecionar o teste correto é fundamental para que os resultados sejam confiáveis.

4. Calcular a estatística de teste e o p-valor

Após definir o teste, calcula-se a estatística correspondente (como t, z, χ² ou F) e, a partir dela, o p-valor. O p-valor indica a probabilidade de observar resultados tão extremos quanto os obtidos caso H₀ seja verdadeira.

• Se p < α, rejeita-se H₀.
• Se p ≥ α, não se rejeita H₀.

É importante lembrar que “não rejeitar H₀” não significa provar que ela é verdadeira, e sim que não há evidências suficientes para descartá-la.

5. Interpretar o resultado

Na última etapa, os valores obtidos são traduzidos para o contexto da pesquisa:

• Rejeitar H₀: há evidência estatística de efeito ou diferença.
• Não rejeitar H₀: os dados não oferecem suporte suficiente para afirmar que o efeito existe.

Uma boa interpretação vai além do p-valor e considera também o tamanho do efeito, o desenho do estudo e suas limitações.

Exemplo

Uma escola deseja avaliar se uma nova técnica de estudo melhora o desempenho dos alunos.

• H₀: a técnica não altera a nota média.
• H₁: a técnica aumenta a nota média.

Após aplicar o método a um grupo de 30 estudantes, o teste estatístico resulta em:

• t = 2,5
• p = 0,02

Como p < 0,05, rejeita-se a hipótese nula. Isso indica que a técnica de estudo provavelmente contribui para melhorar as notas dos alunos.

Conclusão

Os testes de hipóteses permitem transformar intuições e observações em conclusões fundamentadas em evidências. Quando aplicados corretamente, ajudam a identificar efeitos reais, guiam decisões com segurança e reduzem a probabilidade de erros. Compreender seus princípios — desde a escolha do teste adequado até a interpretação dos resultados — é essencial para qualquer análise de dados rigorosa e confiável.