Regressão Linear: teoria e exemplos

Se o gestor de uma empresa precisa determinar a relação exata entre gastos com publicidade e vendas para planejamento futuro, o método de regressão linear será o mais apropriado.

O que é regressão linear?

A regressão linear é um modelo matemático que descreve a relação entre diversas variáveis. Os modelos de regressão linear são um procedimento estatístico que ajuda a prever o futuro. Ele é usado em campos científicos e nos negócios. Nas últimas décadas tem sido usado em Machine Learning.

A tarefa da regressão em Machine Learning é predizer um parâmetro (Y) a partir de um parâmetro conhecido X.

Por que a regressão linear é importante?

Os modelos de regressão linear são muito populares em vários campos de pesquisa graças à sua rapidez e facilidade de interpretação.

Devido à sua capacidade de transformar dados, eles podem ser usados para simular uma ampla gama de relações. Já devido à sua forma, que é mais simples do que a das redes neurais, seus parâmetros estatísticos são analisados e comparados com facilidade, permitindo que informações valiosas sejam extraídas deles.

A regressão linear não é usada apenas para fins de previsão: também tem se mostrado eficaz para descrever sistemas. Se você quer modelar os valores de uma variável numérica, terá uma lista relativamente curta de variáveis independentes e, como você espera que o modelo seja compreensível, é provável que você escolha a regressão linear como sua ferramenta de modelagem.

Tipos de regressão linear

Dependendo dos objetivos do estudo, você pode escolher entre diversos tipos de análise de regressão:

• Simples

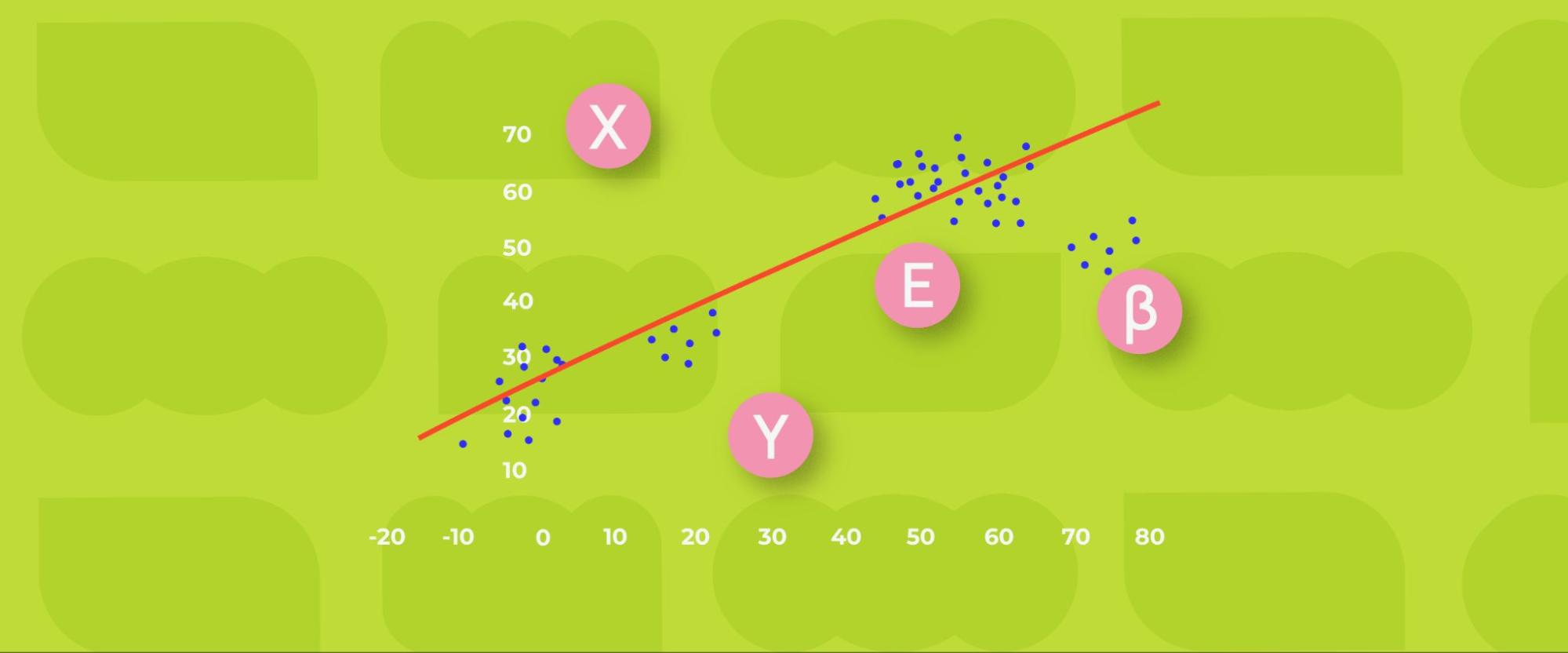
Em uma regressão linear, trata-se de estabelecer uma relação entre uma variável independente e sua variável dependente correspondente. Essa relação é expressa como uma linha reta. Não é possível traçar uma linha reta que passe por todos os pontos de um gráfico se eles estiverem dispostos de forma caótica. Portanto, apenas se determina a localização dessa reta por regressão linear. Alguns pontos seguirão distanciados da reta, mas essa distância deve ser mínima. O cálculo da distância mínima da reta a cada ponto é chamado de função de perda.

A equação de uma linha reta tem a seguinte forma:

Y = β₀ + β₁X + ε,

Onde:

1. Y é a variável independente.
2. β₀ e β₁ são duas constantes desconhecidas que representam o ponto de interseção e a inclinação, respectivamente.
3. ε (épsilon) é a função de perda.

Veja a seguir um exemplo gráfico de um modelo de uma regressão linear simples:

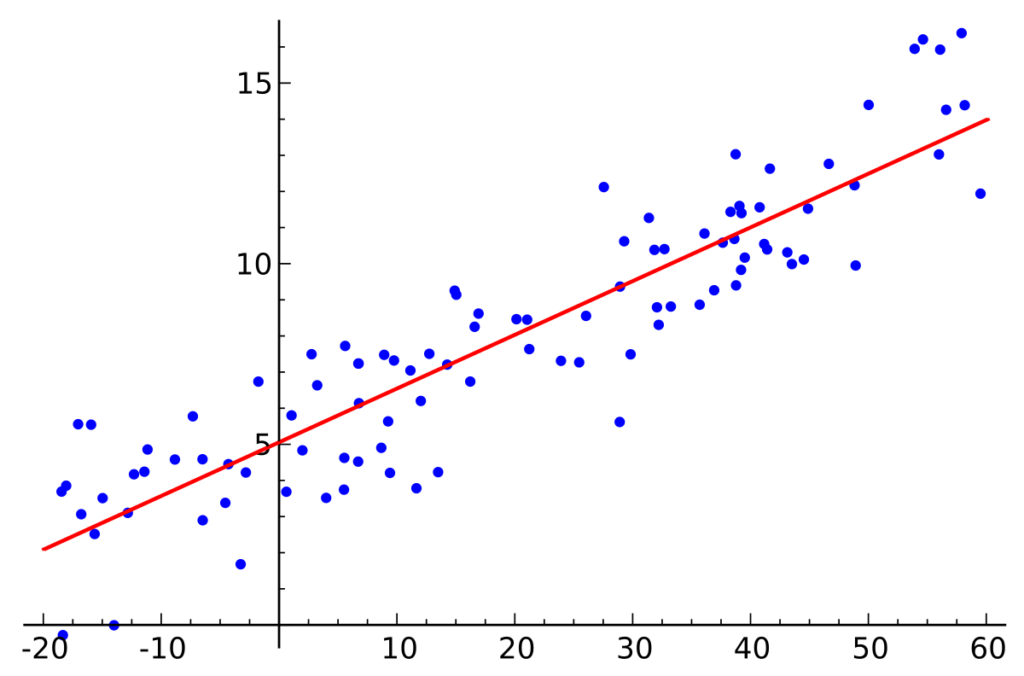
Aplicação da regressão linear simples:

1. Para predizer a colheita em função da precipitação, com a precipitação como variável independente e a colheita como variável dependente.
2. Para saber que nota os alunos obterão em função do número de horas que estudam: aqui a quantidade de horas de estudo representa a variável independente e as notas, a dependente.
3. Para prever o salário baseado na experiência: a experiência se torna a variável independente e o salário, a variável dependente.

Limitações da regressão linear simples:

A regressão linear simples estabelece que existe uma relação entre as variáveis, mas não revela uma relação causal: Y depende de , mas não implica que gere Y.

Se você precisa estabelecer mais do que apenas a existência de uma relação, precisará fazer uma análise adicional.

• Múltipla

A regressão linear múltipla encontra a relação entre duas ou mais variáveis independentes e sua variável dependente correspondente.

A equação de regressão linear múltipla tem a seguinte forma:

Y = β₀ + β₁X₁ +β ₂X₂ +… +βₐXₐ + ε

Onde:

1. Y é a variável dependente.
2. X é uma variável independente.
3. β são coeficientes.
4. ε (épsilon) é a função de perda.

Veja a seguir um exemplo gráfico de um modelo de regressão linear múltipla:

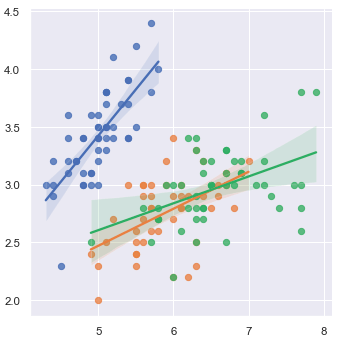
Aplicações da regressão linear múltipla:

Esse tipo de regressão permite predizer tendências e valores futuros. A análise de regressão linear múltipla ajuda a determinar o grau de influência das variáveis independentes sobre a variável dependente, ou seja, o quanto a variável dependente mudará quando mudarmos as variáveis independentes.

Programas para análise de regressão linear

JASP: É um excelente software gratuito de análise de regressão para Windows e Mac. Contém um módulo de regressão com vários métodos de análise de regressão. Com eles é possível analisar facilmente as variáveis que afetam um tema ou área de interesse.

PSPP: É um software gratuito de análise de regressão para Windows, Mac, Ubuntu, FreeBSD e outros sistemas operacionais. Fornece métodos de regressão para estimar um conjunto de dados. Você pode inserir facilmente um conjunto de dados nele e, em seguida, realizar uma análise de regressão. Os resultados da análise de regressão são exibidos em uma janela de visualização de resultados com todos os passos usados.

Statcato: É um software gratuito e portátil de análise de regressão baseado em Java para Windows, Linux e Mac. Para executar este software, é necessário ter o Java instalado.

Jamovi: É outro software gratuito de análise de regressão para Windows, Linux, Mac e Chrome OS. É um software de análise estatística agradável, conciso e fácil de usar, utilizado para tarefas relacionadas à análise de dados.

Exemplos de uso da regressão linear na vida real

Exemplo 1. Suponhamos que precisamos entender a relação entre gastos e receitas com publicidade. Vamos representar isso com um modelo de regressão linear, no qual o gasto com anúncios é a variável independente e a receita a variável dependente. O modelo de regressão seria o seguinte:

Receitas =β₀ + β₁(Gastos com publicidade),

β₀ representa o total de receita esperada sem investimento em publicidade.

β₁ é a variação média da receita total ao aumentar o gasto com publicidade em uma unidade (por exemplo, um real brasileiro).

Se o valor de β₁ é negativo, quanto maior for o gasto com publicidade, menores serão as receitas.

Se o valor de β₁ tende a zero, significa que os gastos com publicidade têm pouco efeito sobre as receitas.

Se o valor de β₁ é positivo, quanto maior forem os gastos com publicidade, maiores serão as receitas.

Em função do valor de β₁, a empresa pode decidir reduzir ou aumentar os gastos com publicidade.

Exemplo 2. A regressão linear também é utilizada na Medicina quando é necessário estabelecer a relação entre a dose dos medicamentos e a pressão arterial dos pacientes.

Para isso, tomaremos a dose como variável independente e a pressão arterial como variável dependente. O modelo de regressão terá a seguinte forma:

Pressão = β₀ + β₁ (Dose),

β₀ representa a pressão arterial esperada quando não são fornecidos medicamentos; a dose é igual a zero.

β₁ é a alteração média da pressão arterial quando se aumenta a dose em uma unidade.

Se β₁ é negativo, a pressão arterial diminuirá ou aumentará a dose.

Se o valor de β₁ tende a zero, a mudança na pressão arterial não se deve a um aumento da dose do medicamento.

Se o valor de β₁ é positivo, então a pressão arterial aumentará se é elevada a dose.

O valor de β₁ permite decidir se modifica-se a dose para o paciente.

Exemplo 3. Os agrônomos medem o efeito dos fertilizantes e a água na colheita, por meio de regressão linear.

O fertilizante e a água são a variável independente e a produtividade é a variável dependente. O modelo de regressão será:

Produtividade = β₀ + β₁ (fertilizante) + β₂,

β₀ indica a colheita esperada sem usar fertilizantes, nem água.

β₁ é a variação média na colheita quando a quantidade de fertilizante é aumentada em uma unidade, supondo que a quantidade de água permanece constante.

β₂ é a variação média na colheita quando a quantidade de água é aumentada em uma unidade, supondo que a quantidade de fertilizante é a mesma.

Com base nos valores de β₁ e β₂, os agrônomos poderão ajustar a quantidade de fertilizante e água para maximizar a colheita.

Exemplo 4. A regressão linear também pode ser aplicada no esporte. Este método permite determinar o efeito de diferentes sistemas de treinamento sobre o desempenho dos jogadores.

Por exemplo, especialistas em Data Science da NBA podem analisar como diferentes sessões de yoga e levantamento de peso afetam o desempenho de um jogador. Tomemos as sessões de yoga e as sessões de levantamento de peso como variáveis independentes e o resultado final como variável dependente. Obteremos:

Desempenho = β₀ + β₁ (Sessões de yoga) + ₂β (Sessões de levantamento de peso),

β₀ representa o desempenho esperado de um jogador que é preguiçoso, não pratica yoga nem levanta pesos.

β₁ é o resultado médio que se obtém ao aumentar em um o número de sessões semanais de yoga, supondo que o número de sessões semanais de levantamento de peso não muda.

β₂ indica a mudança média no resultado alcançado ao aumentar em um o número de sessões semanais de levantamento de peso, sem alterar o número de sessões semanais de yoga.

Dependendo dos valores de β₁ e β₂, os especialistas podem recomendar ao jogador que aumente ou diminua o número de sessões de yoga e levantamento de peso para maximizar seus resultados.

Conclusão

A regressão linear descreve a relação entre várias variáveis: a variável dependente e uma ou mais variáveis independentes. Devido à sua velocidade de criação e facilidade de interpretação, os modelos de regressão linear têm sido utilizados com sucesso em vários setores, desde a Medicina à Agronomia, tanto para fazer previsões quanto para descrever sistemas. Existem programas gratuitos que explicam como fazer para que a aplicação da análise de regressão seja fácil e eficaz.

Se você quer prever o futuro da sua empresa com rigor científico, a EBAC oferece o curso online Profissão Cientista de Dados. Aprenda a trabalhar com diferentes algoritmos e recursos de Big Data e Machine Learning. Domine as principais ferramentas e metodologias, para usar SQL, fazer análise de dados com Python e muito mais. Enquanto aprende, você trabalhará em um projeto profissional, que, ao final do curso, o ajudará a enriquecer seu portfólio. Você também receberá um certificado que vai aprimorar seu perfil profissional.